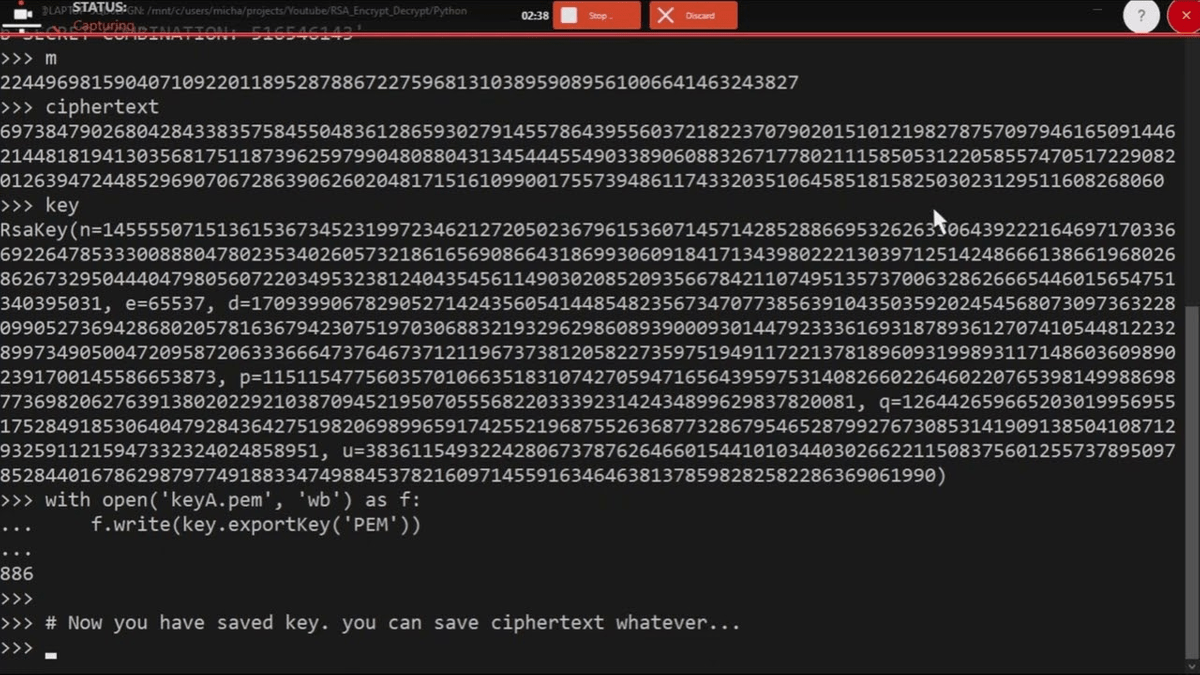
Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). CTF Generator: Low exponent in RSA (for public exponent).This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\). In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution. CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack.In this example, an RSA cipher has used the same message and with three different moduli. CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack.